What’s a Conic?

Circles and parabolas are probably two of the first objects you’ve encountered in your mathematical education. They’re both fundamental, and it’s a wonderful discovery to first learn that they’re in the same family of mathematical objects.

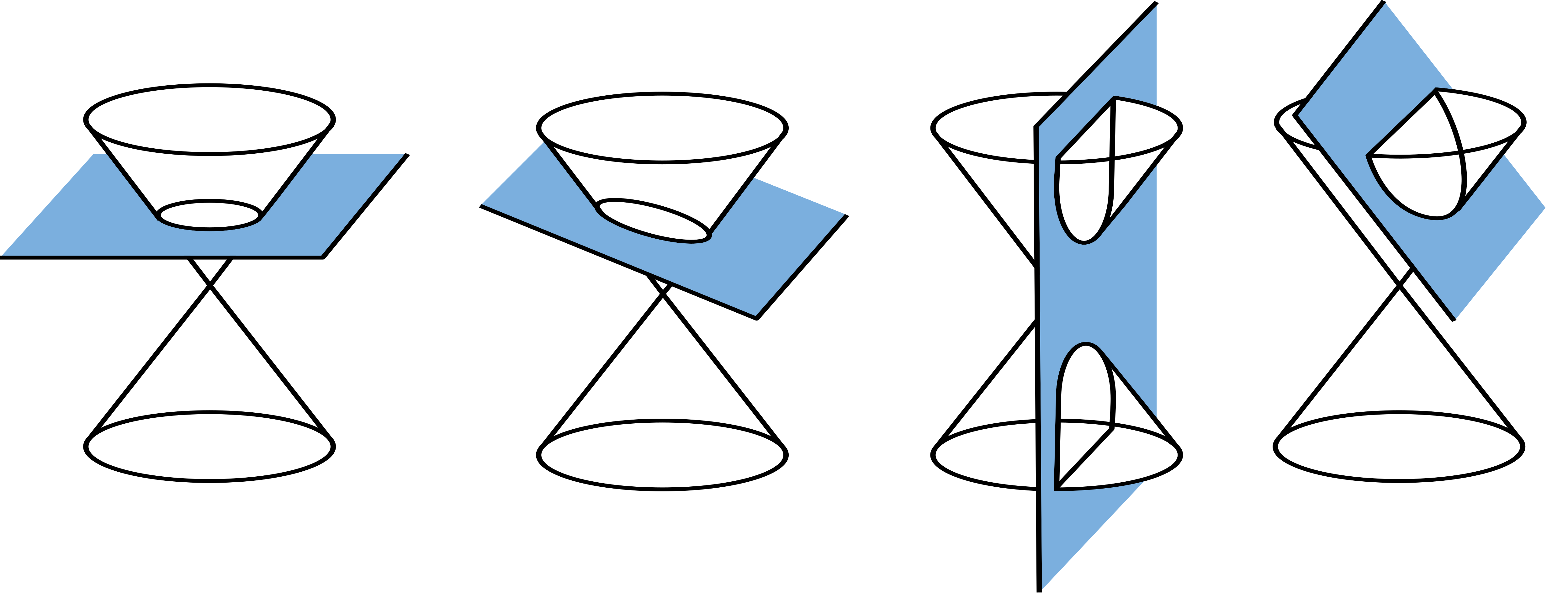
Both circles and parabolas, as well as ellipses and hyperbolas, are conic sections—the geometric objects obtained by intersecting a cone (a double cone, to be precise) with a plane.

Looking at the picture above, you can see that the type of conic formed depends on the angle between the plane and cone.

• Axis of the cone perpendicular to the plane? A circle is formed! Tilt it just a bit to get an ellipse.
• Plane is very steep, cutting through the top and bottom cones? A hyperbola results!
• Plane’s exactly parallel to the wall of the cone? You get a parabola.

In fact, why don’t you play with conics yourself?

Spin and Adjust

There is another possible outcome: the plane might pass through the vertex of the cone. In this case, the intersection might be a pair of intersecting lines, a single line, or just a single point. This case is a degenerate conic, and I’ll ignore it here for the most part.

Algebraic Characterization

The cone is the solution set of the equation $z^2=x^2+y^2$ . The plane, on the other hand, solves $z=ax+by+c$ . Because each of these equations defines a 2-d surface in 3-d space, the set of points that satisfy them both form a 1-d curve in 3-space which can be projected down onto the plane. That’s what’s happening in the right-hand plot above.

What does the solution set look like when it’s written algebraically? Well, eliminate $z$ and take a look at it in 2 dimensions!

We can reparameterize this, instead writing the solution set as the set of points that solves

This is just the solution set of a quadratic polynomial in two variables!

How Many Points?

It’s well-known that it takes exactly two points in the plane to uniquely determine a line. Is there a number of points that can uniquely determine a conic?

Consider again the equation $Ax^2+Bxy+Cy^2+Dx+Ey+F=0$ , but in the six variables $A$ to $F$ . This is a homogeneous linear equation: if $F$ is nonzero (which is always true if the conic is nondegenerate) then we can divide through by $-F$ and relabel:

an equation in five variables.

Linear algebra tells us that it takes five equations in five variables to get a unique solution. Thus, exactly five points uniquely determine a conic ^[1]! Explore this further below in the interactive visualization.

Drag them Around!

A natural question: can we tell what sort of a conic can be formed just from the points, without going back into 3-space with the real cone and plane? We sure can! A number called the discriminant of the conic, which is equal to $B^2-4AC$ , determines the type as follows:

• Determinant positive: ellipse
• Determinant zero: parabola (or degenerate conic)
• Determinant negative: hyperbola

In the visualization, when you hold a point, the colors that appear below represent the discriminant of the conic that will be created if you drop that point there. Yellow will give you a hyperbola, green a parabola or degenerate conic, and blue an ellipse!

Looking Onwards

The three types of conics seem very different: ellipses are closed, while parabolas and hyperbolas open to infinity.

This difference seems massive from our Euclidean perspective, where infinity is like a wall that we can’t see past. However, that isn’t the only way to look at things—the projective plane includes a line at infinity, like the horizon.

If you stand in the middle of a straight highway, the two parallel white lines seem to meet at the horizon. In projective space, we take this idea further: two parallel lines do in fact intersect on this line at infinity! Each family of parallel lines with a different slope defines a point on the line at infinity.

If we think of conics as objects in the projective plane, then there’s only one type rather than three:

• Ellipses don’t touch the line at infinity
• Parabolas are ellipses that lie tangent to the line at infinity
• Hyperbolas are ellipses that cross through the line at infinity, meeting it at two different points

Remarkable! This result is a key theorem in projective geometry. I will prove it in a future post—stay tuned!

Footnotes

[1] This “proof” is just an informal justification, though: it doesn’t account for the nondegenerate case. The formal proof relies on the fact that there’s a bijection between conics and points in five-dimensional real projective space! What does that mean? Well, the five-dimensional real projective space $\mathbb{RP}^5$ is equal to the quotient of six-dimensional Euclidean space (excluding zero) by the multiplicative action of the reals. This means that the point $(a, b, c, d, e, f)$ would be equivalent to the point $k(a, b, c, d, e, f)$ when multiplied by any nonzero real $k$ . You can see that this is the same behavior expressed by a conic!

Each point $(x_i,y_i)$ that the conic passes through is a single linear equation in $\mathbb{RP}^5$ . By Bézout’s Theorem, the intersection of five independent hyperplanes in real projective 5-space is a single point, or equivalently, a single conic!